NUMBERS
We know that when we count we start 1,2 .... . But there are other numbers like 0, negative numbers and decimals. All these types of numbers are categorized in different groups like counting numbers, integers,real numbers, whole numbers and rational and irrational numbers according to their properties. all this have been covered in this chapter
Factors and Multiples tutorial
Tutorial Created by Willbald Mvungi-Ilboru Secondary
Factors of a Number
Find factors of a number
Consider two numbers 5 and 6, when we multiply these numbers i.e. 5 x 6 the answer is 30. The numbers 5 and 6 are called factors or divisors of 30 and number 30 is called a multiple of 5 and 6. Therefore factors are the divisors of a number.
Example 15
Find all factors of 12
Note that, when listing the factors we don’t repeat any of it.
Multiples of a Number
Find multiples of a number
Multiples of a number are the products of a number. For example multiples of 4 are 4, 8, 12, 16, 20, 24, … This means multiply 4 by 1, 2, 3, 4, 5, 6, … .
Example 16
Example
List all multiples of 6 between 30 and 45.
Solution
The multiples of 6 are: 6×1 = 6; 6×2 = 12; 6×3 = 18; 6×4 = 24; 6×5 = 30; 6×6 = 36; 6×7 = 42; 6×8 = 48 and so on.
Therefore, multiples of 6 between 30 and 45 are 36 and 42.
Factors to Find the Greatest Common Factors(GCF) of Numbers
Use factors to find the greatest common factors(GCF) of numbers
G.C.F tutorial
Tutorial Craeted by Willbald Mvungi-Ilboru Secondary
Greatest Common Factor is sometimes called Highest Common Factor. Its short form is (GCF) or (HCF) respectively. The Greatest Common Factor is the largest common divisor of two or more numbers given.
For example if you are told to find the GCF of 15 and 25. First, list all factors or divisors of 15 and that of 25. Thus, factors of 15 are 1, 3, 5, 15factors of 25 are 1, 5, 25
The common factors are 1 and 5. Therefore the GCF is 5.
Example 17
Example1
Find the HCF of 72 and 120.
Solution
We have to list factors of our numbers:
Factors of 72 are 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Factors of 120 are 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120
The common factors are 1, 2, 3, 4, 6, 8, 12, 24.
Therefore the HCF of 72 and 120 is 24.
Another method which can be used to find the GCF or HCF is prime factorization method.
Example 18
Example
Find the HCF of 36 and 48.
Solution
We have to find prime factors of 36 and 48 first
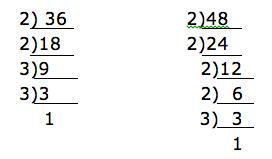
thus, 36 = 2×2×3×3.
48 = 2×2×2× 2×3.
After writing the numbers as a product of their prime factors, take only the common prime factors (prime factors appeared to all numbers). In our example the common factors are 2×2×3. Therefore the HCF of 36 and 48 is 12.
Lowest Common Multiple (LCM)
Lowest Common Multiple is also called Least Common Multiple and its short form is LCM.For example: multiples of 5 are 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, …multiples of 3 are 3, 9, 15, 18, 21, 24, 27, 30, 33, ….
When you look carefully at these multiples of 5 and 3 you notes that 15 had appeared to both. This multiple which appear to both is called a common multiple. If there are more than one common multiples which appeared the smaller common multiple is what is called Lowest Common Multiple.
Example 19
Find the common multiples and then show the Lowest Common Multiple of the numbers 4, 6 and 8.
Solution
Multiples of 4 are 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, …
Multiples of 6 are 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, …
Multiples of 8 are 8, 16, 24, 32, 40, 48, 56, 64, 72, …
The common multiples of 4, 6 and 8 are 24, 48, …
Therefore the Lowest Common Multiple of 4, 6, and 8 is 24.
We can find the Lowest Common Multiple (LCM) of numbers by writing the numbers as a product of their prime factors. The method is called prime factorization.
Example 20
Find the LCM of 24 and 36 by prime factorization method.
Solution
Let us find prime factors of each number by dividing the numbers by their prime factors.
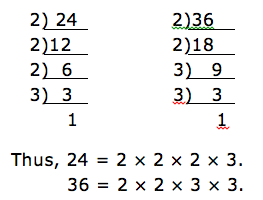
Now take the prime factors which appear to both numbers i.e. 2×2×3 (we take without repeating). We are left with 2 which is a multiple of 24 and 3 which is a multiple 36. We have also to multiply these prime factors left i.e. 2×2×2×3×3. This gives 72. Therefore the LCM of 24 and 36 is 2×2×2×3×3= 72.
Here is a tutorial o n L.C.M
Tutorial Created by Willbald Mvungi-Ilboru Secondary
No comments:
Post a Comment